النسبة الذهبية والنسبة الفاضلة وتوظيفهما في الخط العربي

العلوم الرياضية من حيث هي علوم نظرية لا تتعلق بالمادة، بل بالكمّ والقياس والنسبة، كانت أصولها قابلة لأن تُطبّق في ضروب من الفنون العملية، كما يُطبَّق البرهان في الصناعة أو الرسم أو الخط، إذ إن الاشتراك بين هذه المقادير إنما هو في الصورة، لا في المادة. ولهذا فإن من نظر في علم النسبة، سواء في تسلسل الأعداد أو في تناسب الأشكال، فإنه ينظر في معقول كليٍّ واحدٍ، وإن اختلفت مواده بالحسّ.

ومن هذا الباب يُذكر ليوناردو فيبوناتشي الذي تعلّم في بلاد المغرب، في مدينةٍ من مدن الجزائر كانت معروفة آنذاك بريادة علم الحساب عند العرب. ومن جهة الصناعة التعليمية، كان العرب قد بلغوا في هذا العلم مبلغًا عاليًا، حتى صار التعليم الرياضي عندهم يتجاوز الحس إلى المجرد، والعدد عندهم يُدرس من حيث ماهيته لا من حيث مادته. ولهذا لما درس فيبوناتشي الأرقام العربية، أدرك تمايزها المنطقي من الأرقام اللاتينية، فمال طبعه إلى هذا العلم ميلًا فطريًا، إذ وجد فيه ما يوافق مقتضى العقل من انتظام النسبة.

ثم لما عاد إلى إيطاليا في أوائل القرن الثالث عشر، جمع ما تلقاه من العلوم العددية، وصاغ منها بناءً نظريًا، أشهره ما يُعرف اليوم بتسلسل فيبوناتشي. وأصل ذلك المسألة المشهورة التي عُرضت عليه في مجلس بيزا بإذن من الإمبراطور فريدريك الثاني، في حساب تكاثر الأرانب على فرض شروط مخصوصة: أن كل زوج من الأرانب يولد في الشهر الثاني من ولادته زوجًا آخر، وأنه لا يموت شيء من تلك الأزواج، فكم يكون المجموع بعد سنة؟

والنتيجة المنطقية لهذه المسألة كانت تولّد عددٍ يكون كل حدٍّ فيه حاصل جمع الحدين اللذين قبله، أي: F(n) = F(n-1) + F(n-2)

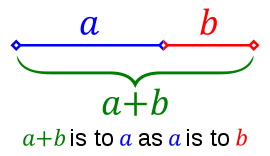
فإذا بدأ التسلسل من ١، ١، كان التالي ٢، ثم ٣، ثم ٥، وهكذا على الترتيب إلى ما لا نهاية له بحسب الإمكان. وهذا التعاقب الرياضي لم يكن مجرد ترتيب عددي، بل كشف عن علاقة نسبية ثابتة بين الحدود، حيث إن نسبة كل حدٍّ إلى الحد الذي قبله تؤول إلى مقدار ثابت يقارب (1.618)، وهو الذي عُرف فيما بعد بـ النسبة الذهبية.

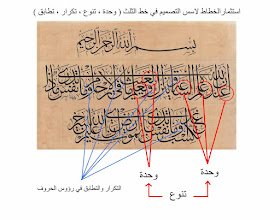
العلاقة بين النسبة الفاضلة في الرياضيات والنسبة الفاضلة في الخط العربي: وحين ننتقل من مجال الكم المجرد إلى مجال الرسم والهيئة، نجد أن تلك النسبة نفسها تتجلى في الصناعة الخطية، لا من حيث الماهية العددية، ولكن من حيث نظام التناسب الهندسي الذي يحكم الحروف والأشكال. فالنسبة الفاضلة في الخط العربي، كما أصلها ابن مقلة، تقوم على مبدأ رياضي لا يختلف في جوهره عن المبدأ الذي تقوم عليه نسبة فيبوناتشي. لأن في كليهما علاقة ضرورية بين المقادير تحفظ الانسجام والاتساق. وإنما الفرق أن فيبوناتشي نظر إلى النسبة من حيث هي تجريد عددي، وابن مقلة نظر إليها من حيث هي تطبيق شكلي على بنية الحرف.

ويمكن بيان هذا بالتحليل الآتي:

1. الألف مرجع للقياس: لأن كل حرف يقاس بالنسبة إلى طول الألف، كما يُقاس في الرياضيات كل مقدار بوحدةٍ ثابتة. فالألف في الخط كـ"الواحد" في الحساب.
2. النقطة مقياس جزئي: وهي كالوحدة الجزئية في القياس الرياضي، إذ تُحدد بها أجزاء الحرف بدقة.
3. الدائرة معيار التناسب: لأن قطرها يساوي طول الألف، فهي تمثل دائرة النظام، أي الحدّ الجامع الذي تُنسب إليه أطوال الحروف وعروضها.
4. الثوابت النسبية بين الحروف: لكل حرف نسبة معلومة بالنسبة للألف والدائرة، وهذه النسب ليست وضعية أو ذوقية، بل موضوعية، لأن الخط الجميل هو الذي تتحقق فيه النسب الصحيحة كما تتحقق في الشكل الهندسي الصحيح. فإذا كانت النسبة في علم العدد هي علاقة مقدار بمقدار على جهة التضعيف أو التجزئة، فإن النسبة في الخط هي علاقة بعدٍ ببعد على جهة التوازن البصري.

ففي كليهما يوجد قياسٌ وتقديرٌ وتوسطٌ بين طرفين: إفراطٍ وتفريط. ولهذا تكون النسبة الفاضلة في الخط مبدأ ضروريًّا في حفظ التناسق، كما تكون النسبة الذهبية مبدأً ضروريًّا في انتظام التكرار العددي. ولما كان كل نظام منظمٍ لا بد له من مبدأٍ أول يقاس به غيره، كان الألف في الخط كالصفر في الحساب: ليس له تأثير في المقادير بعده، لكنه أصلها، ومنه تُستخرج. فكما أن الصفر لا يزيد العدد ولا ينقصه ولكنه شرطٌ لبنية النظام العددي، كذلك الألف في الخط لا يحمل معنىً بذاته ولكنه شرط لبنية النظام الخطي. ومن هنا تتحد الصناعتان في العلة وإن اختلفتا في الصورة